
For the schoolchildren of tomorrow
| Front Page | Welcome | Two | Three | Four | Pentagram | Six | Spirals | The Plot Thickens | Astronomy | 2006 Formations |
 The 'wormhole' formations appeared this year. These were nested sets of crescents, they are sets of circles whose centres swing back and forth as they are made. As the circle radius expands by one unit each step, the circle centre likewise moves along by that same amount (see figure) keeping them all co-tangential: they all touch the same line.
The 'wormhole' formations appeared this year. These were nested sets of crescents, they are sets of circles whose centres swing back and forth as they are made. As the circle radius expands by one unit each step, the circle centre likewise moves along by that same amount (see figure) keeping them all co-tangential: they all touch the same line.
- 20th June, Windmill Hill near Avebury: a pair showing a symmetrical but inverse pattern, one composed of 14 rings.
- 8th July, Uffington, Oxfordshire: Two sets of 14 rings.
- 15th July, Aldbourne, near Swindon, Wiltshire, one set of 21 rings The centre slowly swings back and forth, as the nested crescents are created, twenty-one circles drawn in all
In each of these designs, the 'moving centre' becomes alternately positioned in smoothly-flowing flattened wheat, and then in undisturbed standing wheat. Scrutiny of the photographs shows that nothing has disturbed these centres.
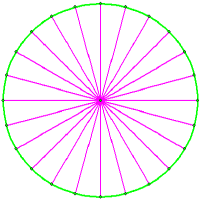
 The perimeter of a circle is divided into nine (at 40° intervals). Setting the compass between two of these points, nine circles are thereby drawn on that circle. The very same process was used to make the 18-fold design of 20th August, 2005. Each of its 'chunks' have four sides.
The perimeter of a circle is divided into nine (at 40° intervals). Setting the compass between two of these points, nine circles are thereby drawn on that circle. The very same process was used to make the 18-fold design of 20th August, 2005. Each of its 'chunks' have four sides.
 The nine-circle construction is repeated, but inscribing the arcs only within the main circle. Two further concentric rings are added, whose radii compare to the outer ring as 4:6:7, so the outer ring diameter must be divided into seven parts, taking four-sevenths and six-sevenths for the extra circles. Notice that the alternate parts of the pattern are 'shaded in' as compared to the previous design. Patterns using seven (or multiples thereof) are quite strongly emphasised this year.
The nine-circle construction is repeated, but inscribing the arcs only within the main circle. Two further concentric rings are added, whose radii compare to the outer ring as 4:6:7, so the outer ring diameter must be divided into seven parts, taking four-sevenths and six-sevenths for the extra circles. Notice that the alternate parts of the pattern are 'shaded in' as compared to the previous design. Patterns using seven (or multiples thereof) are quite strongly emphasised this year.
The two centres here express opposite kinds of 'radiation', with circles coming out of one and straight lines from the other. The main circle diameter is divided into twenty-one equal parts, fourteen between the two foci, and another 3½ such spaces on either side. So, the distance between the foci is two-thirds of the diameter. From one of the foci emanate concentric circles, while from the other come straight lines, creating an interference pattern. It may not be aesthetically pleasing, but they wanted to do it - somewhat as, in the 'parabola' design of 2005, sets of concentric circles and straight lines also interfered with each other.
A 21-fold division was earlier used in the an interference pattern constructed back in 2001 (August 1), where the sides of a triangle were thus divided. Again one felt a bit of a mystery, as to why anyone would want to do that.
We've now seen two formations of 8th July, both using the number 14. We shall see how a third formation, the finest of the year, also appeared on that day.
 Two nests of non-concentric circles share a tangent, which they touch at the same place. As a counter-theme, this central tendency is balanced by two more nests of non-concentric circles, touching a tangent on either side. The diagram shows two sets of nine rings, of radius increasing one step at a time, aligned with two different tangents. A mirror-reflection down its centre line, creates this formation! Outside the two central rings an interference pattern then appears, its central portions erased by the inner circles.
Two nests of non-concentric circles share a tangent, which they touch at the same place. As a counter-theme, this central tendency is balanced by two more nests of non-concentric circles, touching a tangent on either side. The diagram shows two sets of nine rings, of radius increasing one step at a time, aligned with two different tangents. A mirror-reflection down its centre line, creates this formation! Outside the two central rings an interference pattern then appears, its central portions erased by the inner circles.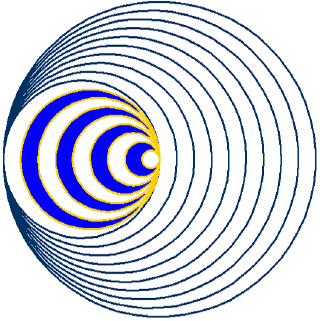 This formation appears as a follow-on from the 'wormhole' designs of the previous weeks, as a metamorphosis of their theme in which inner and outer appear as subtly counterbalanced - a trademark of the Circlemaker masterpieces.
This formation appears as a follow-on from the 'wormhole' designs of the previous weeks, as a metamorphosis of their theme in which inner and outer appear as subtly counterbalanced - a trademark of the Circlemaker masterpieces.
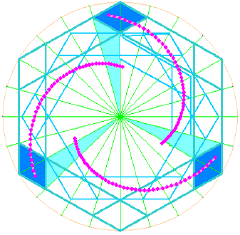
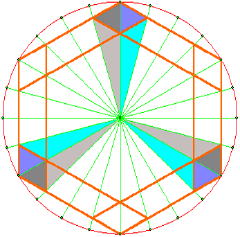
A circle is divided into twenty-four, with radial lines drawn in. A hexagon is inscribed within this. Then, straight lines are drawn parallel to the sides of this hexagon such that each straight line touches the outer hexagon on a radial line. This produces the 'diamond' corners, or rhombi.
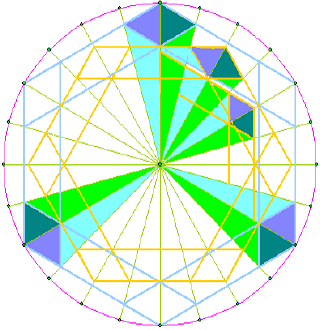 Then, straight lines rotated at 30° are made to touch the inner corners of these diamonds, and extend over two such radial lines, ie at 30° away from the diamond corners. Thus a second hexagon is constructed, which does not quite touch the outer one. The procedure is repeated to create diamonds at its corners, using the 24 radii as before. At this point it may help to shade in the two sets of diamonds or rhombi: only alternate rhombi are counted, three out of six.
Then, straight lines rotated at 30° are made to touch the inner corners of these diamonds, and extend over two such radial lines, ie at 30° away from the diamond corners. Thus a second hexagon is constructed, which does not quite touch the outer one. The procedure is repeated to create diamonds at its corners, using the 24 radii as before. At this point it may help to shade in the two sets of diamonds or rhombi: only alternate rhombi are counted, three out of six.
One iterates this procedure, to make the third and fourth 'skyscrapers'. There is a lovely geometrical progression here, with three logarithmic spirals (contracting in the ratio 4: 3 + ![]() 3 per 30°, so each skyscraper is about 18% smaller than the previous one)
3 per 30°, so each skyscraper is about 18% smaller than the previous one)
Once the final design is completed and the construction-lines all fade away, only then do we notice the remarkable 3-D appearance. Only then are we struck by the solid-looking buildings surging — rather joyfully - out of the ground. This masterpiece of 2006 represents the 'Ground Zero' of New York, where the World Trade Centre towers are being rebuilt. Three towers were destroyed on that fateful day and here they are growing up again!
 After last year's beautiful parabolic design, it seems only logical that the Circlemakers should produce a hyperbola. A hyperbola is a curve that extends out to infinity on each axis. This one had three axes, which means that it had six axes of symmetry. Each axis was measured out to ten units: to construct it, straight lines were drawn joining 10 to 1, 9 to 2, 8 to 3, etc, on adjacent axes.
After last year's beautiful parabolic design, it seems only logical that the Circlemakers should produce a hyperbola. A hyperbola is a curve that extends out to infinity on each axis. This one had three axes, which means that it had six axes of symmetry. Each axis was measured out to ten units: to construct it, straight lines were drawn joining 10 to 1, 9 to 2, 8 to 3, etc, on adjacent axes.
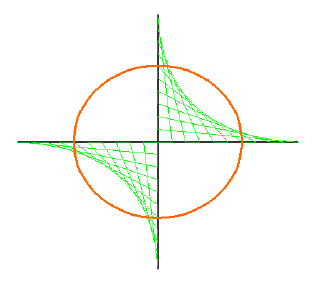 The equation here is y = ± 1/x, with the hyperbola having ten units along its axis. A surrounding circle has radius 6 units. This design has four axes of symmetry. The fields of Oxfordshire and Wiltshire were given mathematically-related formations, though but no-one realised this. I'm writing this in June 2007 and (correct me if I'm wrong) no-one has stated that they were both hyperbolae.
The equation here is y = ± 1/x, with the hyperbola having ten units along its axis. A surrounding circle has radius 6 units. This design has four axes of symmetry. The fields of Oxfordshire and Wiltshire were given mathematically-related formations, though but no-one realised this. I'm writing this in June 2007 and (correct me if I'm wrong) no-one has stated that they were both hyperbolae.
The three conic sections have now been accomplished by the Circlemakers! Earlier, I had written 'Hypermaths does not involve conic sections but only perfect circles ...' (Intro to Crop Circles, The Hidden Form'). First they made an ellipse, but with access denied to its foci, ie its foci were positioned in undisturbed wheat. Then they produced a nest of parabolae in 2005, that were confocal then the next year they made hyperbolae.