
For the schoolchildren of tomorrow
| Front Page | Welcome | Two | Three | Four | Pentagram | Six | Spirals | The Plot Thickens | Astronomy | 2006 Formations |
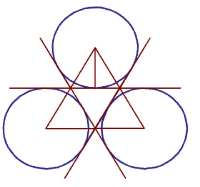
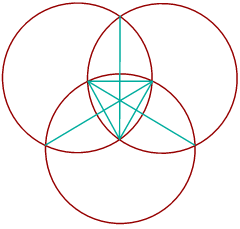 Let us start with the triune template discerned by Bert Janssen: www.bertjanssen.nl/content/cropcircles/reconstructions.html, go into The basis).
Let us start with the triune template discerned by Bert Janssen: www.bertjanssen.nl/content/cropcircles/reconstructions.html, go into The basis). We might well want to call this sacred geometry, on account of its high levels of symmetry and its inner concordance. Three circles are drawn around an equilateral triangle. Thereby three Vesica Pisces are made. Because of this, we recognise that root three is going to be involved in the scale of things: if the triangle has sides of unit length, then the long axis of the Vesica will be
We might well want to call this sacred geometry, on account of its high levels of symmetry and its inner concordance. Three circles are drawn around an equilateral triangle. Thereby three Vesica Pisces are made. Because of this, we recognise that root three is going to be involved in the scale of things: if the triangle has sides of unit length, then the long axis of the Vesica will be ![]() 3.
3.
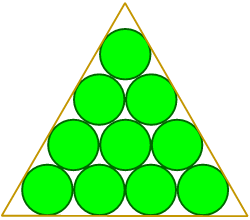
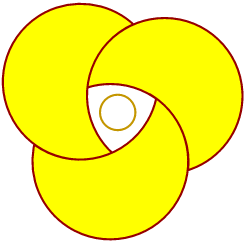 Can you show that the little circle is one-twelfth of the area of each of the others? That circle touches the 'latent' triangle, is held within it (Hint: if the circle has unit radius, then show that the triangle sides are each 2
Can you show that the little circle is one-twelfth of the area of each of the others? That circle touches the 'latent' triangle, is held within it (Hint: if the circle has unit radius, then show that the triangle sides are each 2![]() 3. Squaring that, gives the area of the circles). The Circlemakers have a propensity to give us these integer solutions.
3. Squaring that, gives the area of the circles). The Circlemakers have a propensity to give us these integer solutions.
 No original pictures have survived, and it was therefore convenient that a replica of this same design appeared, ten years later. Alton Barnes, 4 May 2008.
No original pictures have survived, and it was therefore convenient that a replica of this same design appeared, ten years later. Alton Barnes, 4 May 2008.
Usually the Circlemakers don't ever repeat themselves.
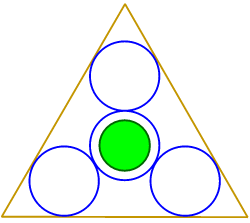
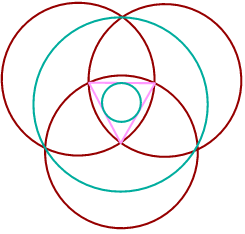 Adding a Circle A year later, the fine symmetry of Meonstoke appeared, having the same basic geometry as the 'sphere within.' Do you agree that its inner circle just touches the central 'latent triangle'? If so, show that the extra circle is four times larger than the central one. Hint: the height of that triangle is thrice that of the radius of the circle inside it. The next design may also help here.
Adding a Circle A year later, the fine symmetry of Meonstoke appeared, having the same basic geometry as the 'sphere within.' Do you agree that its inner circle just touches the central 'latent triangle'? If so, show that the extra circle is four times larger than the central one. Hint: the height of that triangle is thrice that of the radius of the circle inside it. The next design may also help here.

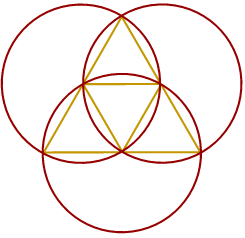 Show that the area of these four triangles compares to that of one of the circles, as
Show that the area of these four triangles compares to that of one of the circles, as ![]() 3 to
3 to ![]() . The outer corners of these triangles just touch the extra circle we looked at earlier.
. The outer corners of these triangles just touch the extra circle we looked at earlier.
 This classic design has stimulated three different web-sites to analyse its structure! On the right is Martin Keitel's depiction showing the unique pattern of its floor-lay (how the wheat was flattened). Each of its three circles would fit exactly in the triangle - i.e., their diameter was half that of the big, surrounding circle: that is the key to solving it. But, how to find where the centres of these are circles located? That is its enigma.
This classic design has stimulated three different web-sites to analyse its structure! On the right is Martin Keitel's depiction showing the unique pattern of its floor-lay (how the wheat was flattened). Each of its three circles would fit exactly in the triangle - i.e., their diameter was half that of the big, surrounding circle: that is the key to solving it. But, how to find where the centres of these are circles located? That is its enigma.
 Martin Keitel has given us a solution which is rather brilliant, martinkeitel.com/cropcircles/harlequin/harle.page3.html and has what might be an advantage of not requiring any work by way of calculation to appreciate - one can merely contemplate it! We start with the two little concentric circles at the centre, and these are in a 3:4 ratio. Both of these are able to pack the triangle - four of one and ten of the other, will exactly fill it! That's the first thing we notice.
Martin Keitel has given us a solution which is rather brilliant, martinkeitel.com/cropcircles/harlequin/harle.page3.html and has what might be an advantage of not requiring any work by way of calculation to appreciate - one can merely contemplate it! We start with the two little concentric circles at the centre, and these are in a 3:4 ratio. Both of these are able to pack the triangle - four of one and ten of the other, will exactly fill it! That's the first thing we notice.
 Taking the larger of these two, doubling its size gives us the three circles of Harlequin, trebling it gives the invisible circle on whose circumference these stand, and quadrupling it gives the big surrounding circle, around the triangle. So there is a pleasant 1:2:3:4 ratio here.
Taking the larger of these two, doubling its size gives us the three circles of Harlequin, trebling it gives the invisible circle on whose circumference these stand, and quadrupling it gives the big surrounding circle, around the triangle. So there is a pleasant 1:2:3:4 ratio here. 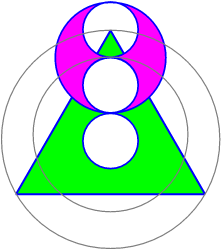 The diagram shows the position of one of Harlequin's circles (in purple), as resting on the unseen circle.
The diagram shows the position of one of Harlequin's circles (in purple), as resting on the unseen circle.
The height of the triangle is equal to the diameter of the invisible circle, Keitel observed, and four of the smallest circles in line will stretch across this. If we started off with a 3:4 ratio, then the unseen or 'latent' circle could be viewed as 12 units. Keitel called his study 'the perfect circular geometry of the Harlequin Triangle.' By contemplating its deep harmonies he was led to the idea of perfection, which is of interest.
 Bert Janssen's construction is a bit more like hard work, www.bertjanssen.nl/content/cropc/winterbourne97.html- in a manner perhaps comparable to the above 'Meonstoke' formation, that appeared two years later. His triune template is woven around the very small circle at the centre of the design. It has the advantage of finding the angle bisectors, that feature prominently in this formation. On this construction, one has to believe that there would be a great deal of 'latent geometry' that would just have to fade away into nothing, leaving only the final design.
Bert Janssen's construction is a bit more like hard work, www.bertjanssen.nl/content/cropc/winterbourne97.html- in a manner perhaps comparable to the above 'Meonstoke' formation, that appeared two years later. His triune template is woven around the very small circle at the centre of the design. It has the advantage of finding the angle bisectors, that feature prominently in this formation. On this construction, one has to believe that there would be a great deal of 'latent geometry' that would just have to fade away into nothing, leaving only the final design.

 Three interlinked circles are called, 'Borromean rings.' For their rich history, see eg www.liv.ac.uk/~spmr02/rings/- none of which are, one is bound to say, quite as good as the Circlemakers' design. For example, the Vikings 'Walknot' ('knot of the slain') was a triangular version of these rings.
Three interlinked circles are called, 'Borromean rings.' For their rich history, see eg www.liv.ac.uk/~spmr02/rings/- none of which are, one is bound to say, quite as good as the Circlemakers' design. For example, the Vikings 'Walknot' ('knot of the slain') was a triangular version of these rings. 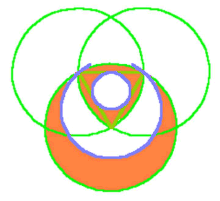 The three rings taken together are inseparable, but remove any one ring and the other two fall apart. Because of this property, they have been used in many fields as a symbol of strength in unity.
The three rings taken together are inseparable, but remove any one ring and the other two fall apart. Because of this property, they have been used in many fields as a symbol of strength in unity.
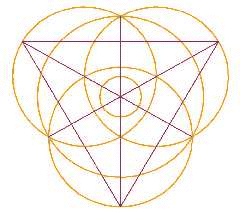
Bert Janssen's triune 'template' is needed for this design, plus three circles whose centres stand on the small, inner circle - i.e., the compass is placed on that inner circle to draw them - so that these cut the other circles at each triangle corner.
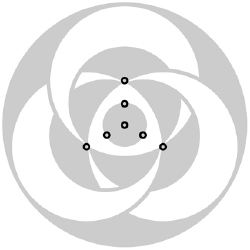 Bert's diagram (kindly provided) highlights the circle centres.This construction uses the ratios 1:7:12 in circle radii - and that is a lot more complex than they were using a few years' earlier.
Bert's diagram (kindly provided) highlights the circle centres.This construction uses the ratios 1:7:12 in circle radii - and that is a lot more complex than they were using a few years' earlier. 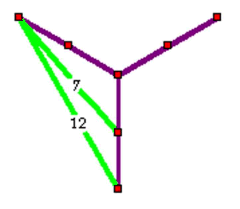 To help find these ratios, a diagram is here given that just fits into the central triangle (Its unit length = radius of centre circle). If the sides of the latter are 12 units, then can you show that these extra circles have radii of 7 units?
To help find these ratios, a diagram is here given that just fits into the central triangle (Its unit length = radius of centre circle). If the sides of the latter are 12 units, then can you show that these extra circles have radii of 7 units?
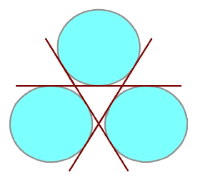

Each line makes a tangent to all three of the circles, i.e. it just touches each of them. Once the distance between each of the three centres is fixed, then their radii have to be ![]() 3/4 times this.
3/4 times this.
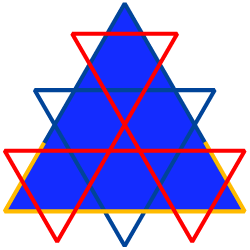
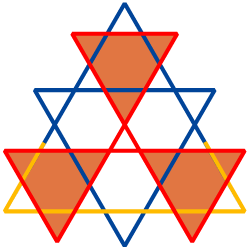 This design, the last to appear in the 1997 season, has a quite blissful feeling to it. In that year a whole series of fractal masterpieces had been laid down, and the Circlemakers had every reason to be pleased with themselves. The triangles are here reverberating to the odd-number scale factors 1, 3, 5 and 7.
This design, the last to appear in the 1997 season, has a quite blissful feeling to it. In that year a whole series of fractal masterpieces had been laid down, and the Circlemakers had every reason to be pleased with themselves. The triangles are here reverberating to the odd-number scale factors 1, 3, 5 and 7.
As the millennium turned, an image of perfect harmony appeared, next to Silbury Hill. It took two nights to develop. A hexagon rotated a half-turn to give a twelve-sided figure, making a twenty-fourfold division of the circle, i.e. 15° intervals. At the centre was a sixfold or ninefold division of the triangle. To quote from Freddie Silva's website concerning this mandala: '… its elements effectively encoding the harmonics of light - 3, 6, 9, 12, 24.' I felt it was so mysterious, that every line of an inner triangle pointed towards a corner of an outer triangle: every sharp corner (30°) of the outer triangles, was being pointed to by an edge of an inner triangle. The big triangle is delicately held, with the circle around it about 10% smaller than that at the perimeter.
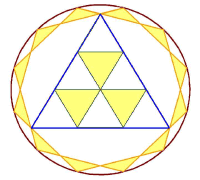
This triangle gives us an opportunity to clarify some elementary matters: one can see that its height is three times the radius of a circle inscribed inside it; and that the lines bisecting the angles which meet in the middle are dividing each other in the ratio of 2:1. for one who has difficulty grasping that the circle around an equilateral triangle has twice the radius of that inscribed within it, this diagram could be just what is needed.
This pattern expresses the Tetraktys, eternal symbol of the Pythagorean order.
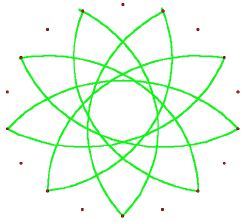
These three 'whirling moons' can be reconstructed using the Tetraktys, as Gerald Hawkins discerned. The arcs here required are of circles having a 3:4 area ratio.

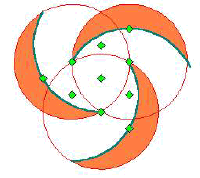
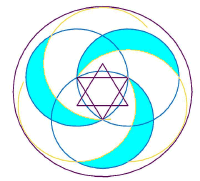
Hawkins presented this insight at the 1998 meeting of the American Astronomical Society at Washington DC, where he gave this construction. I had previously used a hexagon construction, where adjacent tips of the hexagons formed the centres of the arcs. Each lunar-crescent tip gets pointed to by lines, either from the hexagon or in the tetratkys, twice.
A circle is drawn around the whirling moons, to touch them. A hexagon around this will reach the centres of three outer circles. These will be on the slightly larger circle, that was marked into the crop. The larger arcs of the crescent-moons just reach this circle. It's a complex, symphonic design. 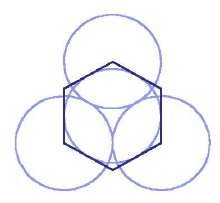
If three circles touch, with a fourth at their centre, and they are all the same size, then an enveloping hexagon around the centre circle can be drawn through the three centres. That is the harmonious theorem expressed in this construction. I wish I'd been taught that at school.
 With a circle divided into 18, draw arcs within it, setting the compass to four of its divisions, without removing the pen from the paper, as it were. That gives one a nine-petalled design. One then gives that a half-turn rotation, and presto!
With a circle divided into 18, draw arcs within it, setting the compass to four of its divisions, without removing the pen from the paper, as it were. That gives one a nine-petalled design. One then gives that a half-turn rotation, and presto!  There is the 18-fold design in all its splendour. One rather lacks a name for this formation. I was foxed by this design, until Allan Brown explained it to me.
There is the 18-fold design in all its splendour. One rather lacks a name for this formation. I was foxed by this design, until Allan Brown explained it to me.
Here you may (or indeed may not) wish to meditate upon the significance of these numbers: nine concerns the process of incarnation, whereby the Sun and Moon meet nine times as the foetus grows in the womb; whereas 18 concerns the synchrony of the Saros cycle, whereby the Sun and Moon have their rhythms interlocked to generate the synchrony of eclipse repetitions.
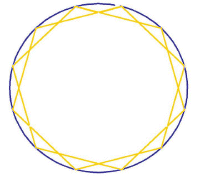
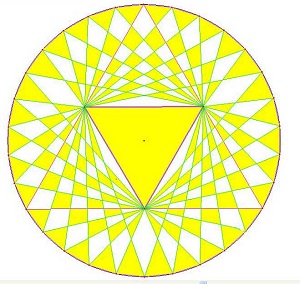
A circle is divided into 30 equal parts, and a triangle placed in the centre. Which lines of this pattern are truly straight, that go right from one side of the circle to the other? The only such lines, are three which form a big triangle touching the circle, as shown. The smaller central triangle is then inscribed within that. All the other lines are just 'glittering irradiations'.
|
To construct this, one would need the ratio of circle radius to the triangle side, see if you can show that this is 2 to |

|
|
To have the three axes of symmetry, the circle had to be divided into multiple of 6, but why 30? There is an aesthetic factor here, whereby this design looks as if the sides of the centre triangle are extended out to the sides. They aren.t quite, the lines aren.t quite straight, but (I suggest) they are nearly enough straight to look good. |
There is the unique triangle where the length of a side divided by its base length equals phi the golden ratio, 1.618. Its base angles are both one-fifth of a circle and its top angle is one-tenth (36o). Mathematicians call it the 'divine triangle'. The golden ratio has long been associated by philosophers with beauty and harmony. The Circlemakers have managed that here, also a circle at the top has a diameter equal to the triangle base. Five lines touch the base of the triangle, and then in the circle above a set of five lines cover the top angle of 36o, perhaps hinting at a pentagram-type motif.
Picture : neX

|
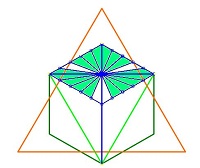
A regular hexagon has a fivefold division made along each of its sides. This is a design which mulls over fivefold versus sixfold symmetries. There are three 'diamond' shapes in that hexagon, |
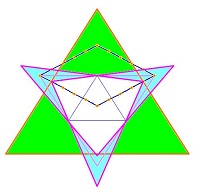
|
one here shown. A big triangle fixes the size of the circle that was laid down, and it cuts the sides of the diamond-rhombus along these fivefold-division points: one side in the ratio of 3 + 2, then again in the ratio of 4 + 1. Mathematically speaking that is the point of this exercise - that a regular triangle concentric with a regular hexagon cuts it in accord with that regular fivefold division. We see how lines flow out from the centre of each rhombus, and suffer mirror reflections as they travel around: two go around the centre, while three go off to the periphery. A regular triangle is inscribed in the hexagon, touching three of its corners. It has triangle-like shapes reverberating around it, inside and outside, held in place by that fivefold rhombus pattern.
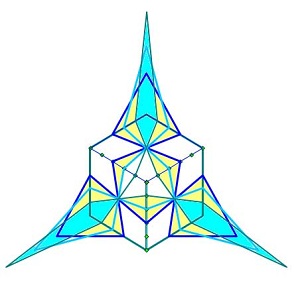
|
At the vertices of a small, centre triangle, all the lines cross. If we say its corners are one unit from the centre, then the hexagon would have corners two units from the centre, and the Big Triangle has (it turns out) corners 3.2 units from the centre. Some lines reflect out to a periphery beyond the circle (they extend out 8/3 units from the centre). The design has three axes of symmetry, buy it also gives us a strangely cubic impression. |
|
Sponsored by Paul Vigay |