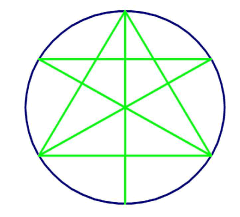
This formation is woven of dark and light triangles, that emerge from the three bisecting diagonals. A unique axis of asymmetry swaps over the dark and light, and is cleverly divided into four equal parts.

The triangles are all similar, having areas in the geometric series ratio 1 : 3 : 9.

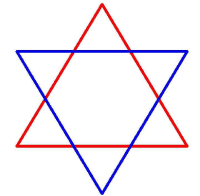The Circlemakers developed the 'Star of David' motif in 1997. This design has an enveloping hexagon around the outside, touching its 18 corners at equal intervals.

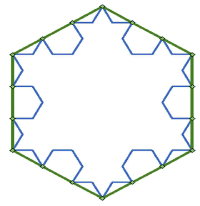
Koch discovered his 'fractal' process back in 1905, and its first three steps are as shown.

A more complicated iteration is of this fractal was published by Gerow and Holbrook in 1996 - their diagram shows a Koch-star going though three steps of iteration. A formation appeared in August of 1997, in which the circlemakers developed the theme by using the same Koch fractal line to generate a pattern within.

This always appears to me as one of their supreme masterpieces. It is twelvefold in its division of the circle and has six axes of symmetry. There are three Koch-fractal bars on the outside and six on the inside. The later are pointing inwards, and stand on a hexagon which has been rotated at a 30° angle to the outer structure. Those within are shrunk, and to help find the scale-factor let's compare the two stars in the diagram. Can you show that one has twelve times the area of the other?

The Dolphins (or 'Scimitars') appeared within two concentric circles having a 3:4 ratio. I found a construction based on dividing the two circles into 6 in the usual way, here shown. I did have to admit, however, that they came out looking a bit thin by this method.

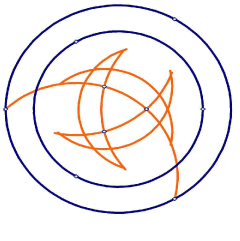A different version was found by Bert Janssen. This used two concentric triangles one four times larger than the other.

Quoting from his instructions: 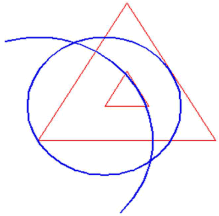'Construct a circle with it's centre in the left corner of the large triangle and with its perimeter just touching the side of the small triangle. Now do the reverse! Construct a circle with its centre in the left corner of the small triangle and with its perimeter just touching the large triangle. The two circles overlap and form a crescent'. www.bertjanssen.nl/content/cropcircles/geometry.html

This is neat, and moreover gives us the two circle arcs in the ratio of 2:3 and the Circlemakers do like these integer ratios. There is a problem with his construction in that it doesn't well connect up to the surrounding circles.

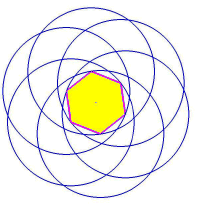
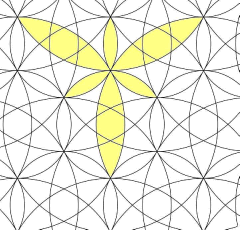Twelve circles make up this formation: nine meeting at the centre, and another three concentric upon it. There are three strong axes of symmetry. The 'hemp leaf' effect comes when two circles of unit radii have one-sixth overlap of their circumferences; or, a distance of root three between their centres. This repeating grid, (from Martineau,. Altair Design, 2000) gives us some insight into the design.

Six arcs here mark out a twelvefold division of the circle - see figure. The arcs are octagonal, they use a one-eighth division of the circle. The basis of this design was a twenty-four fold division, as shown in the second diagram: this includes the centres from which the arcs were drawn. Using this diagram, draw in the one-eighth arcs. Also, the distance across the centre, between opposite arcs, should be the same as the one-twelfth interval. Six and eight are factors of 24. We see how the knot moves round, clockwise.

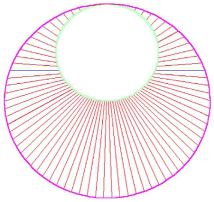There are altogether 13 x 6 = 78 rays which converge towards the 'heart' of the Cambridge 'angel', so she is in a sense lunar as the number 13 pertains to the Moon. The centre of these rays is one-third of the diameter from the top. There seems to be only one straight line going right through this centre, and that line was horizontal, here shown in blue. I counted 47 rays below this line, from which one may derive a total of 78 as the original division of the circle. The radius of a circle is further divided into sixths, to construct her head and shoulders.

Let's quote from Charles Mallett, writing on the Crop circle Connector: "Gog and Magog have once again been chosen to receive a rather simple, but nevertheless incredibly stunning crop circle event, this time of such majestic beauty and harmonious proportion that, for this writer, it's set far apart from the bulk of the English crop formations in 2001. This exquisite, overtly feminine work leaves one with a feeling of almost child-like awe. For me this 'angel' is possibly one of the most attractive and inspirational crop glyphs to have ever graced the magical lands of England."

He counted 75 'rays' which is correct, insofar as the three at the top are not visible. He described the 'ray' tracks as being razor-sharp, about six inches wide, and as having alternate directions of flattening.

Rhombi and hexagons are string onto a charming necklace. We need a hexagon lattice to construct it. The overall pattern is twelvefold rather than sixfold, however, and why is that? It is because the triangles at the centre have suffered a half-turn (i.e., 30°) rotation with respect to the outer ones. These inner triangles are larger, scaled up by a factor of 3 if we include their outer layer. The design has six axes of symmetry, and the three different hexagons which appear have their areas as 4, 12 and 100.

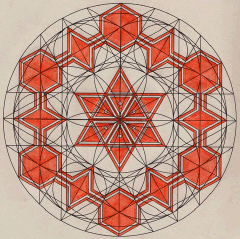The sides of the central 'Star of David' reach out to touch corners of the outer hexagons. This may remind us of the Triune Mandala (June 1st, 2000: West Kennet Longbarrow) where lines used in the centre design reached out to touch key points on the outer frame. Thus outer and inner are linked together. A more intricate reconstruction by Allan Brown is also shown. Note that a single circle touches both outer and inner designs. A sixfold pattern will normally express harmony, whereas a twelvefold design is more to do with wholeness and integration.

The Author of this remarkable design must surely also have made the very comparable triangle-hexagon design one month earlier (Windmill Hill, Wiltshire, June 2005), as some kind of practice run. Its hexagon-motifs have a half-turn rotation with respect to each other, making a twelvefold design altogether. That construction had only one axis of symmetry.

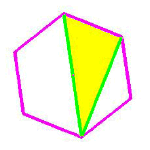The first formation of the season, it appeared in oilseed rape. Draw two lines between the corners of a regular hexagon, as shown. These, the two radii, are in the ratio of 2 to 3. Draw circles around each of the six corners using them. Voila! Colour in the crescent moons.

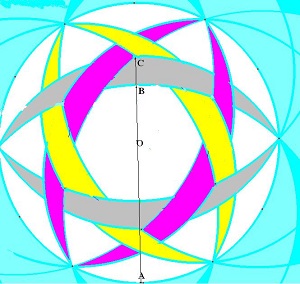
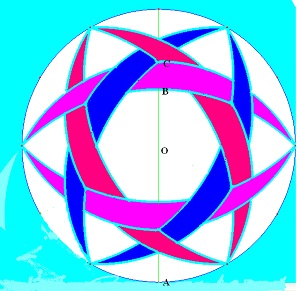
This design is reminiscent of the Scimitars (or 'dolphins') of 24 July 1999, , clearly the same team has designed it - but, the circle is here divided into twelve. At the centre of the image one can faintly see a repeat of the first step - the drawing of six arcs, each starting from one-quarter way round the circle. If the circle has unit radius, then these arcs are of 2 radius (on the diagram, OA is one and AB is 2). The big question is, how are the other arcs to be drawn so that they exactly interlock, as shown? We are startled to note that AC in the diagram turns out to be equal to phi , the golden ratio. How did that happen? Phi turns up in pentagram geometry but one hardly expects it in a sixfold hexagonal structure.

Bisecting the radius OA gives a point, from which the second arc may be drawn. So the secondary arcs are all drawn on a circle concentric with the first but of half its radius. If the first arcs were of 2 length, these next lot have shorter radii of 5/2. In Warwickshire a 'Crown of Thorns' motif appeared, with a gleam of the golden ratio.

Sponsored by Paul Vigay

Web creation by Digital Phenomena Ltd Web hosting by My-Hosts.com