A sphere fits inside a cube. The volumes of this sphere and cube must therefore be as  to 6. If the cube is inside another sphere, see if you can show that its surface area is thrice that of the sphere within.

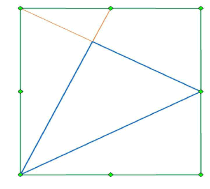
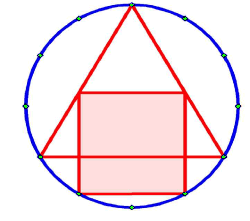A square fits inside a triangle and a sphere. Dividing the circle into twelve, we notice how the triangle and square fall on these points. The square turns out to have times the area of the circle. It divides the triangle into a top part which has one-third the area of the whole. It's a theorem not in Euclid, to be sure (Ground measurements of the formation were made by Andreas Muller, as confirm the reconstruction here given).

Back in 1990, croppies were evaluating the quintuplets: patterns of four surrounding a central circle. The Circlemakers were exploring the idea of tangents, of lines that just touched.

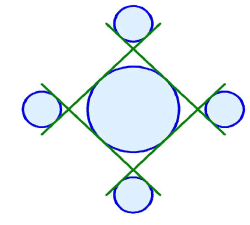
The square pattern set up by the four tangents is pretty obvious, but then a more remarkable octagon - pattern emerges. It looks as if all of the small triangles are identical in this diagram. For that to be so, the centres of the small circles have to be at a distance of twice the radius of the big one, from its centre. The circle-sizes are in the ratio 1 : 1 +2.

Thus the first-beginning of Hypermaths appeared as delicately touching tangent-lines, noticed by John Martineau. I consulted circle-geometer Allan Brown over this, and he agreed that this early formation would bear the above interpretation

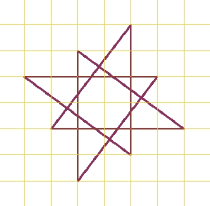
This one's my favourite. It comprises merely a 3:4:5 triangle, rotated through four steps. Or, a rope is divided into eight equal sections with knots, each five units as shown on the grid, pegged out to make the pattern. Or, one starts from the enveloping square around the perimeter which is divided into eight equal sections, then moving around, three sections at a time, will weave it out. Why should doing this produce a 3:4:5 triangle? It does, that's for sure. The eight little triangles around the centre are six times smaller than the big ones, and the two central squares have areas one- fifth that of the enveloping square. An asymmetric octagon forms its centre. Or, is it woven out of rhombi, of four rhombus-shapes? 

The picture (the School of Athens, by Raphael) shows Euclid sketching out what must surely be, the Compass Rose.

This iterative pattern had square sizes decreasing as one, ½ and 1/6^th, each with its centre on the corner of the bigger one. This made their total area double that of the main square (checkout its equation, A + ¾(3A/4 + 12A/36) = 2A where A is area of the main square) - and, its total perimeter, just treble! The Circlemakers have a remarkable knack of finding these whole-number solutions. Persons without interest in mathematics merely derive an aesthetic delight from the shapes, without apprehending the just-so nature of the ratios. This design enjoys both rotational and reflective symmetry. The crop was flattened in two different directions giving the remarkable 3-D effect www.korncirkler.dk/cccorner/universe3.html. A sister-formation appeared a month earlier: www.korncirkler.dk/universe/windmill2.jpg (July 16).

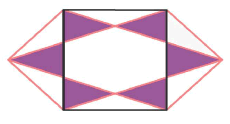Looking at this formation gave a 3-D effect, as if one were seeing a hexagon in perspective.'

The formation itself was quickly regarded as another optical illusion design, which has been a major theme for the 1999 season,' commented Stuart Dike. At its centre was a square: if the six triangles shown are all equal, as they appear to be, then they are all golden, i.e. have base angles of 72° or one-fifth of a circle - (strictly it's 71.6°, the angle whose tangent is three). 

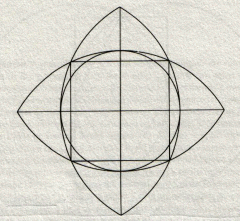
The diagram shown is an 'ancient construction for squaring a circle, creating a circle whose circumference approximated the perimeter of a square' (Michael Schneider, A Beginner's Guide to constructing the Universe 1995). It was a 'traditional diagram of temple foundation in India' (Michell, Dimensions of Paradise, diagram also from there). The formation had a different design, with arcs from corners of a square drawn through adjacent corners. This gives a square and circle having the same area, while the previous design gave more of an agreement in terms of their circumferences. In both cases the agreement was within a few %. These two traditional methods of squaring the circle, by area versus circumference, are treated in Michell's Dimensions of Paradise.

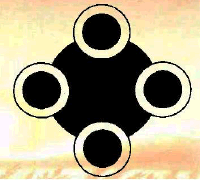
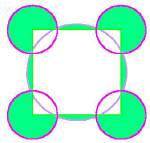
The same area here appears in the central circle and in the sum of four circles (their outer rims); it is also that of the latent square, as specified by the four circle-centres. Does this equality also apply to the circle perimeters? Check this using the accurate silhouette here (drawn by Peter Sørensen). 

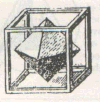
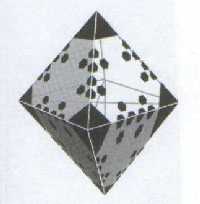
Moving into three dimensions, an Octahedron is made up of triangles. One just needs to cut out the pattern here laid down, and fold it up! NB the smallest units here are all perfect hexagons (Steve Alexander picture, Freddy Silva diagram). See also www.korncirkler.dk/universe/jays1.jpg

This design begins with arcs from four corners of the circle, of the same radius as it, which meet in the middle (Figure a). Then, if this radius is eight units, successive arcs are then drawn of seven, six etc. units down to 3. Of especial interest here is the middle symmetry position where four equal 'octagonal arcs' meet (Figure b). 

These octagonal arcs will not precisely coincide with the arcs drawn by the above method, as neither will the small arcs in Figure 'a' (which make one-sixth divisions of the circle), however the difference is small and within the tolerance of the thickness of the lines. This construction is thus a study in approximation. 

One can imagine a craftsman and mathematician conversing. The former would like to make a stained-glass window, and appreciates how the pattern's strong, fourfold structure will tend to give people a reassuring sense of stability. She or he would like to divide the radius by eighths for this construction, and is that good enough? The arcs look as if they are equidistant, after all. The mathematician appreciates how the sense of 'sacredness' of sacred geometry comes from the way these approximate solutions are closely converging. He explains how the circle is divided by 1/6^th and 1/3^rd parts in 'a' and by octagonal arcs in 'b,' and how the latter division by 8^ths will give the central arcs too small by a mere 2%, and the smallest arcs (Figure a) to small by 3%, these being well within the tolerance of the line-width. 

This shape is what mathematicians call a 'curve of pursuit'. Imagine that four ants are at the corners of a square, and each starts pursuing a neighbouring one. Thereby each one traces out a logarithmic spiral. They remain at corners of a square, which is shrinking, and rotates around the centre at an accelerating rate. All four have to move at the same speed, so that the paths of each chasing ant and its target remain perpendicular.

Its not very clear how one would construct this shape, because the distances between adjacent square-corners are not the same.

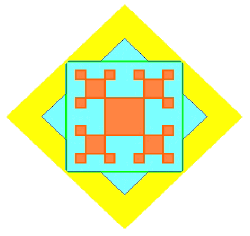
Two large concentric squares of flattened wheat had a one-eighth rotation between them. Within these, two more squares, likewise concentric, have half of their area. The corners touch the sides. Therefore, there is a 2 scale factor, so that the areas of those within are half those without. 
Inside the main square, a progression takes place, where the little squares of flattened wheat in the corners double in length as they move towards the centre. Because their dimensions double, their areas increase as the square: one, four, sixteen. Thus, mathematically speaking, the purpose of this formation, is to contrast the square and square roots of two.

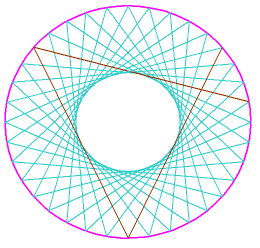A 36-fold division of a circle is here used, and 18 'cubes' lie within it in a hexagonal pattern. Regular triangles could have been generated by moving around the circle twelve steps at a time, but the Circlemakers have here gone thirteen steps at a time, in order to link up all the points. Thus after three steps they have overshot by 30° or one-twelfth of a circle.

The Moon goes round the zodiac every month, and meets up again with the Sun, and each time it does this it has moved round about 30° from its previous position. This might be a helpful analogy.

Use of this odd number means that every point gets touched once in 36 steps, i.e., the pattern starts to repeat after 36 moves. Other prime numbers will also do this, whereas even number intervals only touch half of the points, as one follows the line round.

Concentric circles are placed on the intersection-points. Their radii don't have any simple ratios, eg the outermost two are in the ratio sin30°/sin25° or, one is about 18% larger than the other (Their radii are approximately as 60, 66, 74, 84.5, 100).

This procedure makes every angle at the periphery equal to 50°. Moving towards the centre, the apex angle of each triangle increases by 10° at each step - so the next one in, had there been another layer, would be 90°: i.e., those straight lines extended, staying within that inner circle, make squares! All the lines meet at right-angles on the innermost circle. A ring of 36 right-angles are surrounding the centre. Thanks to Steve Brown for guidance on this one.

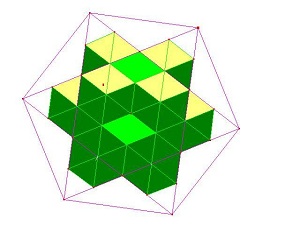
	A hexagon-star is inscribed in a hexagon, with a triangle lattice built up from a sixfold division of the sides. Shading it in then gives a stunning 3-D 'cube' effect. Remarkable 'wheat-texture' effects were here used, to give the shading.

The number Four, the first square number, reconciles the two forms of mathematical growth, being both 2+2 and 2x2, and it represents the human instinct for symmetry and order by dividing the compass onto four points and the year into four seasons. It is at the foundation of civilisation, settlement and rectangular land division. It is the foursquare number of solid earth as opposed to formless heavens.

Sponsored by Paul Vigay

Web creation by Digital Phenomena Ltd Web hosting by My-Hosts.com