In the Vesica Pisces, each centre stands on the other's circumference. Thereby, One becomes Two. Its axis has the length of root three, as compared to the circle radii.

Repeating this process inside the Vesica and at right-angles gives us an inner circle that is one-third the radius of the outer one, which may help us to get a handle on the  concept. See if you can show that four circle-sizes are here used, of areas as 1, 4, 9 and 12. This design has a curiously hypnotic quality.

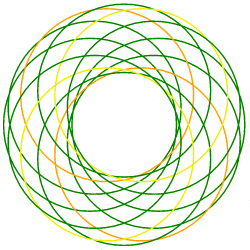If we gradually rotate the Vesica design, in six steps, this gives us the Torus of '97; where the outer circle has thrice the radius of that within.

There seems to have been only one photograph of this one. Its design has six Vesica shapes, rotated as with the Torus. Composed of 48 rhombi, it has an outlying circle thrice the area of that within.

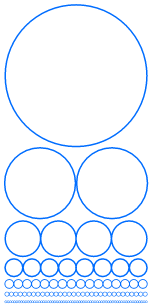A straight line emerges from the division of circles, and there are finally thirty-two tiny circles along that line: one could call this design, two to the fifth. A repeated sub-division takes place, starting from the primal unity. It expresses the geometric progression 2⁰ 2¹ 2² 2³ 2⁴ 2⁵, doubling each time, or 1, 2, 4, 8, 16, 32, where the standing corn signifies even-numbered powers! One can draw a line through its centre, that makes a tangent to ten different circles at once.
The 'pentium' computer chip is so-called because it has a 32-based structure, i.e. 2⁵ . Before that computer chips had a 16-fold design, and in a year or two the 64-based chip is due to arrive. Computers use binary logic.

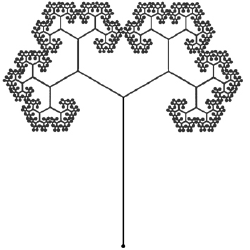A year later, the Circlemakers produced a different kind of binary fission, and this time it had a two to the fourth (2⁴) motif: a tree with four steps of branching, having 16 fruits.
It branched at one-third angles (120°) and its branch-lengths made golden ratios. A reconstruction of this 'golden tree' by Allan Brown is here shown, containing about 20 iterations. Does its boundary resemble that of the formation? The different branches grow to just touch each other, and it is only the phi-ratio which does this: no wonder Mother Nature likes using it (The Golden Ratio, Mario Livio, 2002).

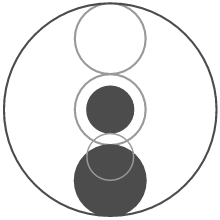This expresses the 2 : 3 ratio, but altogether it has ratios of 1 : 2 : 3 : 9, where 1 is the interval between the circles and 9 is the radius of the surrounding circle. Thus, seen and unseen touch each other.

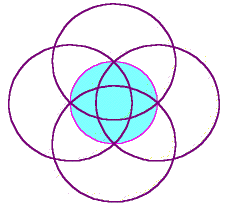
We construct four interlinked Vesica Pisces formations around a circle as shown. Their radii will then be 2 times that of the centre circle, with each arc intersecting the centre circle one quarter of the way round. If an outer circle is then put through the intersection points, this outer circle will be a bit less than double the radius of the inner circle.

The book Crooked Soley, a Crop circle Revelation by Allen Brown and John Mitchell was concerned with this formation, but did not give this construction, making no mention of Vesica Pisces nor of the 2 ratio. But, one of the constructions it gave may lead to the same result. It affirmed that the ratio between outer and inner circles was just 2:1, so the whole question of the construction used was not at all clear.

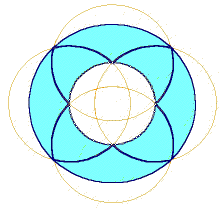
These arcs are then rotated at five-degree intervals, to give 72 arcs going each way, with 18 replications of our original diagram. Arcs both outside and inside the two concentric circles all have to fade away and the basic template thereby emerges. As there are 18 circle-centres per quadrant, so likewise are there 18 crossover-lines per strip, going from inner to outer surface, and there are 72 of these 'strips', giving a total number of 'squares' thereby generated equal to the fourth power of 6 provided one counts all the triangular edge-shapes along boundaries as halves (3): that's what Allen Brown did. Clearly, the ratio between outer and inner circles has to be exact, for this quite large number to be valid.

A sixfold design was inscribed onto this template by the Circlemakers. Here is a different one, to give an idea of how it works. The wheat field allowed no access to the centre or even near it for construction. Only Steve Alexander flew over and photographed it, during the few brief hours of its existence. Allan Brown then discerned and drew its underlying structure.

792 squares were left standing, and this gives the /2 ratio when divided by 504, the total number of laid-down squares. The figure - kindly supplied by Allan Brown, from his book-cover - indicates how these laid-down squares could be counted. That ratio is within 0.04%, which is precise enough to look intentional. It would be less exact, had one more or less tuft remained standing. We are here dealing with a multiple of the basic 22:7 pi-ratio. The number 5040 is mentioned and used in Plato's 'Laws' as having an ideal meaning, and the authors of Crooked Soley found this to be relevant.

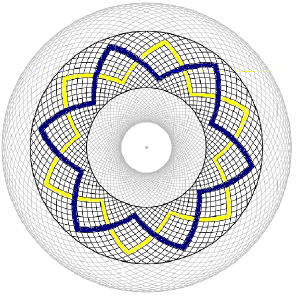
Note that the outermost part of this pattern is hardly 'formatted' with squares. The best and only published image is that published in Crop circles, Signs, Wonders and Mysteries by Steve and Karen Alexander 2006, p.181. However, from this writer's special request, Steve most kindly dug up another image from his fly-over, taken at a better angle than that published, and here it is! This is a close enough resolution to see that the 'slices' do not all have the same thickness. However it does look like an exact 2:1 ratio between inner and outer circles, which is problematic for the analysis given here.

As there are 18 circle-centres per quadrant, so likewise are there 18 'squares' per strip, going from inner to outer surface, and there are 72 of these 'strips', giving a total number of 'squares' thereby generated equal to the fourth power of 6 (try counting them!). This theme was developed remarkably by John Michell and Allan Brown in their book "Crooked Soley, a Crop Circle Revelation". The radii as specified above have to be quite exact, for this large number to have a meaning.

A sixfold design was inscribed onto this template by the Circlemakers. Here is a different one, which may, admittedly, not be quite so sublime. The field allowed no access to the centre to draw this formation. Our acquaintance with this presentation has depended upon just two people: Steve Alexander, who flew over it and photographed it - for no-one visited it, during its very brief existence - and Allan Brown, who discerned and drew its underlying structure.

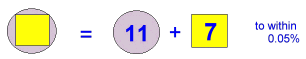The ratio of laid to unlaid 'squares' in this torus design, was 11 to 7. We can express this as the area-ratio between a circle and square that just fits within it; and likewise, a quarter of the circumference of a circle, and its radius, make that ratio. The same pi-ratio is expressed in the Great Pyramid slope angle, as its height to base ratio, giving its slope angle of 51 51'.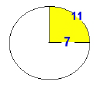

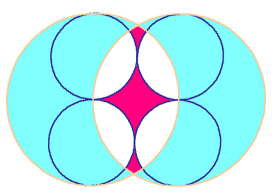A braided pattern was woven on a square template. The same pattern, half-size, then spiralled in towards the centre, in eight braids. The construction design given by Ohayv may not be very credible, and we here prefer the indications given by Allan Brown.

A Vesica Pisces design has circles of half the size packed inside, as shown. Let us suppose that the pattern unfolds with all of these small circles thus touching. An interlinked sequence of Vesica Pisces at right angles to each other is thereby constructed. In this diagram, the yellow-coloured small circles represent the flattened wheat, while the others merely define the pattern. The pattern of wheat left standing is shaded in red.

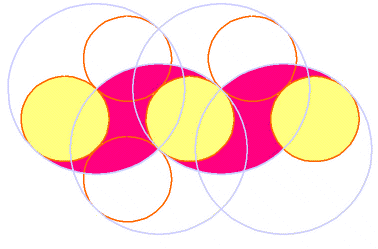
Outer and inner boundaries are constructed around this iterating pattern, their widths being intervals inherently present in the design. Taking the small circle diameter as unit measure, the interval between flattened wheat circles (yellow) is 2-1, and this gives the outer band thickness. There are smaller gaps between the larger circles, equal to 5-2, and these define the thickness of the inner boundary. Thus the decorative art of the Circlemakers emerges from a sense of delight in the maths, whereby they wanted to give expression to key ratios inherent in this Vesica-Pisces pattern.

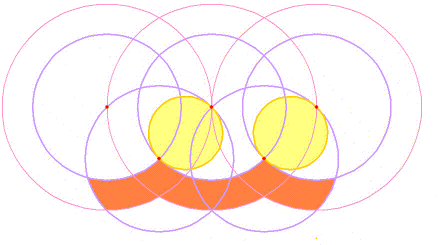At the centre of this design lie eight small circles having prominent central tufts of wheat, marking out a circle identical in size to these Vesica-Pisces circles, whereby the outer and inner designs reflect each other.

The outer boundary is constructed by enlarging the upper set of large circles on our diagram by 2, doubling their area. Thereby a further set of 'Vesica Pisces' appear. There are fifteen Vesicas present in the construction matrix for each side of the big square. These extra large circles are now eight times the area of the little circles. Some part of this iterating design might be used decoratively, eg on a subway wall? The entire matrix would have to be in place before any wheat could have been laid down.

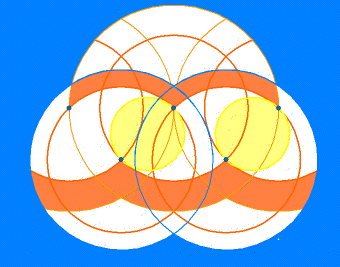An interlocking geometric matrix underlies this pattern, suggesting the existence of an advanced but little known school of decorative art, having a subtle understanding of the Principles of Harmony.

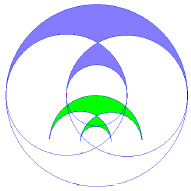
A joyful geometry shows birds in flight. A Vesica Pisces design is thrice-iterated - the Dutch artist Escher would have been proud of it. These three swallows are flying out from an infinite series expansion! The basic design has an elegantly simple 1:2:3 scale in its circle radii, from the smaller one at the centre of the Vesica to the larger one around the outside. A huge number of lines had to be 'rubbed out' to make this design, which may not have been too easy in a wheatfield.

Just colour in the swallows! And thank Bert Janssen for 'seeing' this pattern. He discerned how the inner circle of the 'second' swallow was replicated as the two first circles behind the first swallow 'wings'. The 'heads' have to be added in, as do the 'flight path' balls. And the position of these balls conveys the impression of a gentle curve in the flight path - following a curve in the field tractor lines.

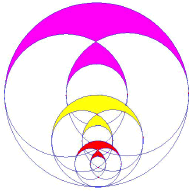
A circle is divided so that it has 24 equally-spaced points on its circumference. From each of these points on the circle one goes a quarter of the way around (i.e., counting six points) and then draws an arc. A pleasant small circle in the middle will then appear. One colours in alternate squares inside the 'eye', and then colours in curved lines outside it, to make the pattern. A lot of lines need to be rubbed out to reach the final design.

The 'eye' at the centre, enclosed by two arcs, may look a bit like a Vesica Pisces - but it isn't. One can show that the ratio of the little circle formed at the centre, to that around the outside, is 1 -  2; or, that the ratio of the outside circle to the small centre circle, is 1 +  2! Neat, eh? For a Vesica pisces that ratio has to be  3.

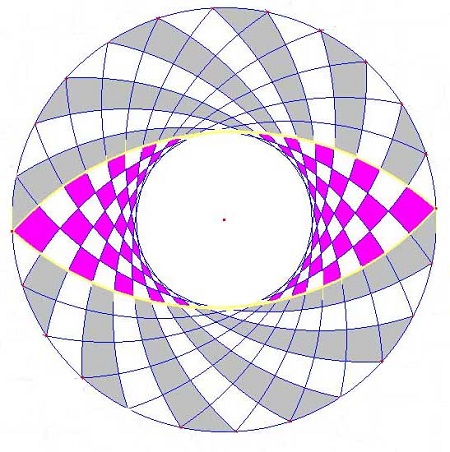
This geometrical recipe may not explain how the shape looks so mysterious and distinctive. How did it get to swirl round like that? And, where did that lovely cascade of curved-rhombi - first one, then 3, then 5, then 7 and lastly 9 little flecks hugging the central circle - where did that come from? Who dreamed up such a thing? That is the genius of the Circlemakers, to derive something so expressive from quite simple maths.

Sponsored by Paul Vigay

Web creation by Digital Phenomena Ltd Web hosting by My-Hosts.com