
For the schoolchildren of tomorrow
| Front Page | Welcome | Two | Three | Four | Pentagram | Six | Spirals | The Plot Thickens | Astronomy | 2006 Formations |
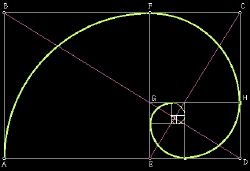 The geometric spiral appears in sea-shells, e.g. the Nautilus here shown, and is called a logarithmic spiral. It never reaches its centre, and its shape always stays the same however much it is enlarged.
The geometric spiral appears in sea-shells, e.g. the Nautilus here shown, and is called a logarithmic spiral. It never reaches its centre, and its shape always stays the same however much it is enlarged.  Its distance from the centre increases by a fixed proportion per turn, or for each quarter-turn. The spiral shown increases by phi, the golden ratio, every quarter-turn: the squares as they revolve shrink by phi every time.
Its distance from the centre increases by a fixed proportion per turn, or for each quarter-turn. The spiral shown increases by phi, the golden ratio, every quarter-turn: the squares as they revolve shrink by phi every time.
The two diagonals drawn in show the radius distance of this spiral: they are at right-angles to each other, and we can see how each successive radius-distance shrinks by phi as the spiral revolves inwards.

A huge triple-spiral appeared in 1996. Each of its three arms expanded by the square of thegolden ratio per 90° turn.  Thus, it moved outwards, or shrunk inwards, faster than the above 'golden' spiral - it expanded by one extra power of the golden ratio, compared to the above figure. A geometric spiral always holds the same angle to its radius-line (or strictly, a tangent to the spiral at the point where the radius line crosses, keeps that same angle). I found that this triple-spiral more-or-less did that, for most of its layout (its angle was 59°), using a diagram of it prepared by Paul Vigay (1). By contrast, a spiral formation which appeared three weeks earlier opposite Stonehenge (www.lucypringle.co.uk/photos/1996/uk1996ay.shtml),while no less magnificent - it became the most visited crop circle ever,with over 15,000 visitors - wasn't a geometrical spiral, i.e. it did not maintain a fixed angle to its radius-line. It was more biological in its shape.
Thus, it moved outwards, or shrunk inwards, faster than the above 'golden' spiral - it expanded by one extra power of the golden ratio, compared to the above figure. A geometric spiral always holds the same angle to its radius-line (or strictly, a tangent to the spiral at the point where the radius line crosses, keeps that same angle). I found that this triple-spiral more-or-less did that, for most of its layout (its angle was 59°), using a diagram of it prepared by Paul Vigay (1). By contrast, a spiral formation which appeared three weeks earlier opposite Stonehenge (www.lucypringle.co.uk/photos/1996/uk1996ay.shtml),while no less magnificent - it became the most visited crop circle ever,with over 15,000 visitors - wasn't a geometrical spiral, i.e. it did not maintain a fixed angle to its radius-line. It was more biological in its shape.
 Six years later, the circlemakers came up with a slow, meditative spiral, which made three rotations, expanding by phi at each rotation (as near as one could tell). We saw how the above 'golden spiral' expanded by
Six years later, the circlemakers came up with a slow, meditative spiral, which made three rotations, expanding by phi at each rotation (as near as one could tell). We saw how the above 'golden spiral' expanded by ![]() per quarter-turn, or
per quarter-turn, or ![]() 4percomplete rotation. So, this 'sacred spiral' was expanding bysix powers of phi more slowly than the 1996 triple spiral.
4percomplete rotation. So, this 'sacred spiral' was expanding bysix powers of phi more slowly than the 1996 triple spiral.
 The same geometric spiral has here been fitted, both to a galaxy spiral, and to a formation (13 June 1999, Newton St Loe). It roughly fits, except for the outermost circle.
The same geometric spiral has here been fitted, both to a galaxy spiral, and to a formation (13 June 1999, Newton St Loe). It roughly fits, except for the outermost circle.
This spiral is doubling in size in just under one rotation.

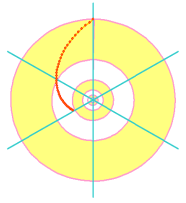 A nest of concentric circles keep halving in size. They go as a half, quarter, eighth and - just about - a sixteenth of the outer rim (we can just see the last one). They point to an infinity within. The shapes are continuous geometrical spirals, that move through each circle per sixty degree turn. There are twelve of these spirals. For a spiral contracting from the outer rim, halving its radius each sixty degrees, its equation is r=R/2
A nest of concentric circles keep halving in size. They go as a half, quarter, eighth and - just about - a sixteenth of the outer rim (we can just see the last one). They point to an infinity within. The shapes are continuous geometrical spirals, that move through each circle per sixty degree turn. There are twelve of these spirals. For a spiral contracting from the outer rim, halving its radius each sixty degrees, its equation is r=R/2![]() /60
/60
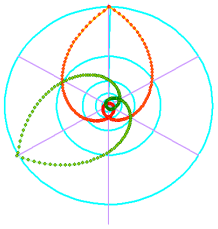
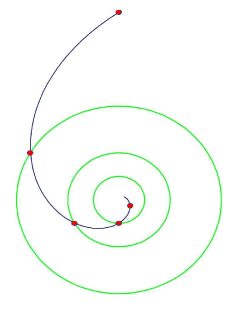 where R is the outer rim radius and the turn angle
where R is the outer rim radius and the turn angle ![]() is in degrees. The figure shows the spiral moving inward. That spiral is on an infinite journey, ever moving towards the centre. Each dot marks sixty degrees of turn, halving its radius. Only three of its five circles are shown.
is in degrees. The figure shows the spiral moving inward. That spiral is on an infinite journey, ever moving towards the centre. Each dot marks sixty degrees of turn, halving its radius. Only three of its five circles are shown.
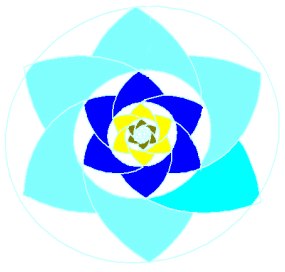

Twelve of these are then combined. Only ten are here shown, as it may help to see it unfinished - otherwise it might look too easy! The rest is just colouring-in.
This shape has rotational symmetry, but not reflective symmetry:i.e., it lacks any axes of symmetry.
After constructing the logarithmic spirals, the Author would have needed to rub out quite a few sections. You may need several attempts to get this right! Thereby we discern four concentric rings of a lily-pattern, containing an infinity within. Alternate layers rotate in opposite directions, and so the shape has rotational but not reflective symmetry: it lacks any axes of symmetry. As a work of art, one feels that its process of becoming is as interesting as the final product. See also Freddy Silva's discussion of this deeply original little masterpiece.
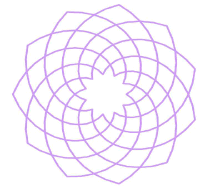
There is a different kind of spiral, that moves not by any ratio or proportion, but by a fixed amount at each step. This is called an Archimedes spiral. I always thought the Archimedes spiral was boring, until I saw how the Circlemakers used it. Twenty-two equilateral triangles surrounded the open circle. Then another ring of 22, at the same distance, and so on, whereby the triangles gradually grow flatter as they move outwards.
The basic structure was 11-fold. Without taking one's pen off the paper, tracing out these spirals will yield the 11-fold design as shown. One then has to perform a half-turn rotation of this entire design to obtain the full, twenty-two fold mandala (2).
The great thing about an Archimedes spiral is that it does reach the centre, unlike the geometrical spiral we looked at earlier: if one here extrapolates the lines back to the centre, a perfect heart-shape is revealed. This formation is woven of twenty-two 'hearts'. Its construction implies a division from the centre into forty-four equal angles. Some saw the ![]() ratio in the way a circle divided into 44 expanded through 14 concentric rings, which reduces to a 22:7 ratio.
ratio in the way a circle divided into 44 expanded through 14 concentric rings, which reduces to a 22:7 ratio.
 |  |  |
Others compared it to the sunflower's spiral, which is likewise an Archimedes-type spiral, but is not symmetrical in the same way.
 |  |
 The first four rings were contained or implied within the central circle, i.e. the formation began on its fifth ring. There were 22 triangles in this ring,and one can show that each must therefore have had a base angle of 60.3°- i.e., they were as close to equilateral as made no difference. Strictly speaking, as Michael Glickman observed, the sides of each of the triangles were gently curved (3).
The first four rings were contained or implied within the central circle, i.e. the formation began on its fifth ring. There were 22 triangles in this ring,and one can show that each must therefore have had a base angle of 60.3°- i.e., they were as close to equilateral as made no difference. Strictly speaking, as Michael Glickman observed, the sides of each of the triangles were gently curved (3).
A Star-heptagon fits well into this formation - as a couple of croppie-geometers have observed (4). That will define its inner and outer limits to within an astonishing 0.1% (5).
These concordances built into this formation, may help us to apprehend the notion of perfection. 'Sacred' geometry may mean that various symmetries are somehow deeply present within it, and that they affect us in some way. The number seven features in its basic pi-ratio (44 divisions and 14 rings), then again in the star-heptagon. See if you can show that the design has equilateral triangles around the centre.

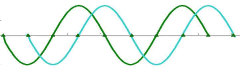
 Sine and cosine waveforms (i.e., out of phase by 90°) went through two cycles. But, the formation did have an impressive 3-D appearance and it did haveten steps laid out, and these inevitably reminded croppies of the human DNA chain, which makes one rotation through ten steps (each step twisted36° from the previous).
Sine and cosine waveforms (i.e., out of phase by 90°) went through two cycles. But, the formation did have an impressive 3-D appearance and it did haveten steps laid out, and these inevitably reminded croppies of the human DNA chain, which makes one rotation through ten steps (each step twisted36° from the previous).
All human DNA turns the same way, clockwise like a corkscrew (called, a 'right-handed' turn). Now look at the 'DNA' agriglyph design and which way is it turning? You will probably see it as turning anti-clockwise (or, a 'left-handed'turn). Clearly, this is something to reflect upon.
Thanks to Stott Onstott for use of his Triple-spiral image, to Steve alexander for the Sacred Spiral and to Stuart Dike for Spiral Mandala.
References
tan-1 (11/2) = 60.3°
sin (/14) = 2/9, to 99.9%
